"PID Kontrol ve Algoritması" sayfasının sürümleri arasındaki fark
| (3 kullanıcıdan 23 ara revizyon gösterilmiyor) | |||
| 1. satır: | 1. satır: | ||
''Açıklama'' | ''Açıklama'' | ||
| − | ''Kategori: | + | ''Kategori: Kontrol Sistemleri'' |
| + | |||
| + | ''Yazar: Mustafa SAVURAN'' | ||
---- | ---- | ||
| 7. satır: | 9. satır: | ||
'''Kontrol sistemleri''': | '''Kontrol sistemleri''': | ||
| − | | + | Kontrol sistemlerinin amacı sistemden alınmak istenilen çıkış değeri ile sistemin verdiği çıkış değeri arasındaki farkı bulmaktır.Bulunan bu fark değeri ile sistem üzerinde kontrol gerçekleştirmektir. Bu farka error (hata) denir. Kontrol sisteminde, sistemin girişi değiştirilerek error değeri en aza indirilmeye çalışılır. |
| − | '''P'''roportional-(Oransal),'''I'''ntegral-(İntegral),'''D'''erivative-(Türev) controller, ölçülen değer(process value) ile istenen ayar noktası(Setpoint) değeri arasındaki | + | '''P'''roportional-(Oransal),'''I'''ntegral-(İntegral),'''D'''erivative-(Türev) controller, ölçülen değer(process value) ile istenen ayar noktası(Setpoint) değeri arasındaki error değerini hesaplar. Setpoint olarak belirlenen değer ile motor hızı, sıcaklık yada herhangi bir girdiden alınan değer farkı alınır. |
| − | '''Error | + | '''Error''' = Setpoint(SP) - Process value(PV) |
| − | + | Error değeri oran, türev ve integrali alınarak çarpılır. Çıkış devresine yeni değer aktarılır. Bu yeni değer sistem içerisinde kıyaslanır. Bu işlem, error 0 ya da minimuma yakın bir değer alana kadar devam eder. | |
[[Dosya:pid-controller-diagram.png|thumb|center|500px|PID Kontrol Blok Şeması-1]][[Dosya:pro3.png|thumb|center|500px|PID Kontrol Blok Şeması-2]][[Dosya:34.png|thumb|center|500px|Hata Grafiği]] | [[Dosya:pid-controller-diagram.png|thumb|center|500px|PID Kontrol Blok Şeması-1]][[Dosya:pro3.png|thumb|center|500px|PID Kontrol Blok Şeması-2]][[Dosya:34.png|thumb|center|500px|Hata Grafiği]] | ||
| 20. satır: | 22. satır: | ||
P=Kp*Error | P=Kp*Error | ||
| − | + | Proportional sistemdeki error değerini (Kp) katsayısı ile çarparak setpoint kısmına yakınlaştırıp, küçültmeyi hedefler. Bu işlem, error değerini hızlıca düzeltir ancak çıkışta salınım yapma ihtimali artar. | |
[[Dosya:pro2.png|550px|thumb|left|Şekil 1-Proportional ile Kontrol Grafiği]][[Dosya:Proportional2.png|540px|thumb|center|Şekil 2-Proportional ile Isıtıcı Kontrol Grafiği]] | [[Dosya:pro2.png|550px|thumb|left|Şekil 1-Proportional ile Kontrol Grafiği]][[Dosya:Proportional2.png|540px|thumb|center|Şekil 2-Proportional ile Isıtıcı Kontrol Grafiği]] | ||
| − | + | * Kp değeri arttırılırsa error değeri hızla azalır. | |
| − | + | * Kp değeri düşük olursa salınım azalır ancak Şekil 1'de görüldüğü gibi Kp=1 değerinde error minumum şekilde devam eder ve hedef noktaya ulaşma süresi artar. | |
| − | + | * Kp değeri yüksek olursa error çok çabuk düzeltilir ancak setpoint değerini hızlı bir şekilde geçer.Bu yüzden salınımları önlemek için Kp değeri yüksek seçilmemelidir. | |
| − | + | * Şekil 2 de görüldüğü gibi bazen (Kp) değeri ne kadar yükseltilirse yükselsin setpointe ulaşılamaz. Ayrıca Şekil 2'de t=2 zamandan sonra ortamda bir değişikliğin oldugunu, bu değişikliğe proportional kontrolünün nasıl tepki verdiği gözlenmiştir. | |
== Integral Kontrol== | == Integral Kontrol== | ||
| 36. satır: | 38. satır: | ||
error_sum+=error | error_sum+=error | ||
| − | + | İntegral error değerinin alanını bulmak anlamına gelir. Bu işlem her bir periyottaki error katsayı (Ki)değeri ile çarpılarak toplanır. Setpoint değerinin altında yaptığı error değerinin alanı kadar setpoint değerinin üst kısmında da salınım yapar. | |
| + | İntegral çok fazla artmadan sınırlandırılması gerekir. Sürekli toplandığı için integral çok artarsa tekrar azalmasını beklemek zaman alır. Bu yüzden integrali sınırlamak sistemin çabuk toparlamasını sağlayacaktır. | ||
[[Dosya:Integral.png|500px|thumb|left|Şekil 3-İntegral ile Kontrol Grafiği]][[Dosya:Integral2.png|610px|thumb|center|Şekil 4-İntegral ile Isıtıcı Kontrol Grafiği]] | [[Dosya:Integral.png|500px|thumb|left|Şekil 3-İntegral ile Kontrol Grafiği]][[Dosya:Integral2.png|610px|thumb|center|Şekil 4-İntegral ile Isıtıcı Kontrol Grafiği]] | ||
| − | + | * Sadece integral ile kontrol yapılırsa toplam error değeri kadar setpoint değerinin üstüne çıkar. Setpoint üzerinde toplam error değerini tekrar hesaplar ve setpoint altında toplam error değeri kadar salınım yapar. Bu nedenle sonsuz bir osilasyon değeri elde edilir. | |
| − | + | * Eğer (Kp) değeri ile (Ki) değeri aynı anda hesaplanırsa başlangıçtan setpoint değerine kadar (Ki) değeri, sürekli error değerlerini toplama içerisinde olduğu için büyük bir error değeri oluşacaktır. Bu nedenle (Kp) değerini belirli bir noktaya getirip, (Ki) değerini (Kp) değerinden sonra başlatmanız gerekir. Böylece oluşacak salınımlar büyük oranda azaltılmış olur. | |
== Derivative Kontrol == | == Derivative Kontrol == | ||
D=Kd*Error (d/dt) | D=Kd*Error (d/dt) | ||
| − | + | Derivative zamana bağlı değerin değişimi ile ilgilidir. Sistemde gerçekleşen değişim sırasında gerçekleşecek değişimi fark eder ve sistemi istenen değerin üzerine çıkmaması için yavaşlatır. | |
[[Dosya:PD.png|500px|thumb|center|Şekil 5-PD Kontrol]] | [[Dosya:PD.png|500px|thumb|center|Şekil 5-PD Kontrol]] | ||
| 53. satır: | 56. satır: | ||
[[Dosya:PID.png|500px|thumb|center|Şekil 6-PID Kontrol ile Isıtıcı]] | [[Dosya:PID.png|500px|thumb|center|Şekil 6-PID Kontrol ile Isıtıcı]] | ||
| − | + | Şekil 6'da Proportional, Integral ve Derivative kulanılmıştır. Verilen grafikte değişken bir ortamda (Kp), (Ki) ve (Kd) katsayılarına farklı değerler verilerek sinyallerin oluşturduğu hareketler gözlenmiştir. | |
| − | == | + | == Referanslar == |
| − | http://fabacademy.org/archives/2014/students/shooshtari.ali/week16/images/PID-Without-a-PhD.pdf | + | [http://fabacademy.org/archives/2014/students/shooshtari.ali/week16/images/PID-Without-a-PhD.pdf fabacademy.org] |
| − | https://www.wescottdesign.com/articles/pid/pidWithoutAPhd.pdf | + | [https://www.wescottdesign.com/articles/pid/pidWithoutAPhd.pdf Şekil 1-2-3-4-5-6/Blok Şeması-2] |
| − | https://www.youtube.com/watch?v=f-BA1Ijnxz0 | + | [https://www.youtube.com/watch?v=f-BA1Ijnxz0 video] |
23:56, 2 Mayıs 2021 itibarı ile sayfanın şu anki hâli
Açıklama
Kategori: Kontrol Sistemleri
Yazar: Mustafa SAVURAN
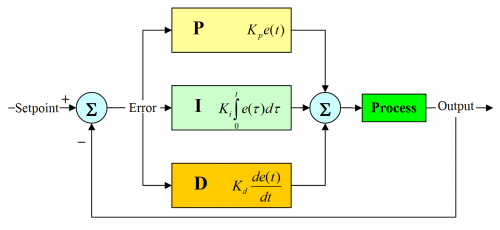
Kontrol sistemleri:
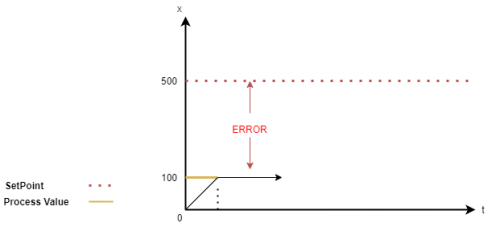
Kontrol sistemlerinin amacı sistemden alınmak istenilen çıkış değeri ile sistemin verdiği çıkış değeri arasındaki farkı bulmaktır.Bulunan bu fark değeri ile sistem üzerinde kontrol gerçekleştirmektir. Bu farka error (hata) denir. Kontrol sisteminde, sistemin girişi değiştirilerek error değeri en aza indirilmeye çalışılır.
Proportional-(Oransal),Integral-(İntegral),Derivative-(Türev) controller, ölçülen değer(process value) ile istenen ayar noktası(Setpoint) değeri arasındaki error değerini hesaplar. Setpoint olarak belirlenen değer ile motor hızı, sıcaklık yada herhangi bir girdiden alınan değer farkı alınır.
Error = Setpoint(SP) - Process value(PV)
Error değeri oran, türev ve integrali alınarak çarpılır. Çıkış devresine yeni değer aktarılır. Bu yeni değer sistem içerisinde kıyaslanır. Bu işlem, error 0 ya da minimuma yakın bir değer alana kadar devam eder.
İçindekiler
Proportional Kontrol
P=Kp*Error
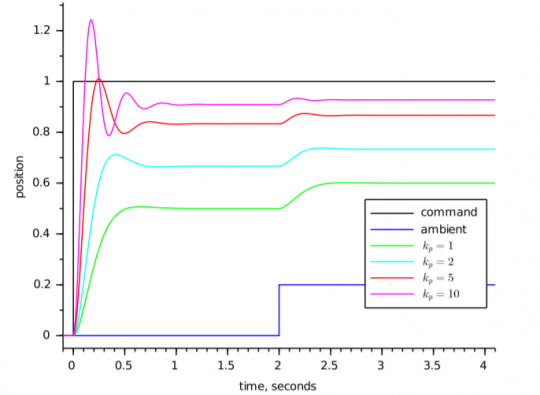
Proportional sistemdeki error değerini (Kp) katsayısı ile çarparak setpoint kısmına yakınlaştırıp, küçültmeyi hedefler. Bu işlem, error değerini hızlıca düzeltir ancak çıkışta salınım yapma ihtimali artar.
- Kp değeri arttırılırsa error değeri hızla azalır.
- Kp değeri düşük olursa salınım azalır ancak Şekil 1'de görüldüğü gibi Kp=1 değerinde error minumum şekilde devam eder ve hedef noktaya ulaşma süresi artar.
- Kp değeri yüksek olursa error çok çabuk düzeltilir ancak setpoint değerini hızlı bir şekilde geçer.Bu yüzden salınımları önlemek için Kp değeri yüksek seçilmemelidir.
- Şekil 2 de görüldüğü gibi bazen (Kp) değeri ne kadar yükseltilirse yükselsin setpointe ulaşılamaz. Ayrıca Şekil 2'de t=2 zamandan sonra ortamda bir değişikliğin oldugunu, bu değişikliğe proportional kontrolünün nasıl tepki verdiği gözlenmiştir.
Integral Kontrol
I=Ki*Error
error_sum+=error
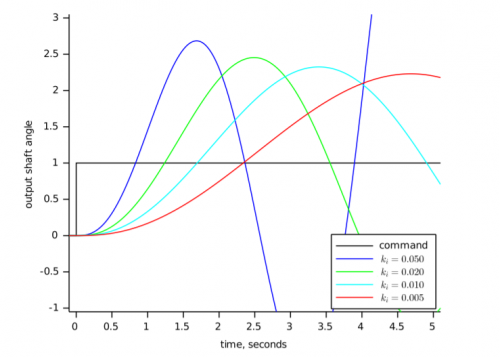
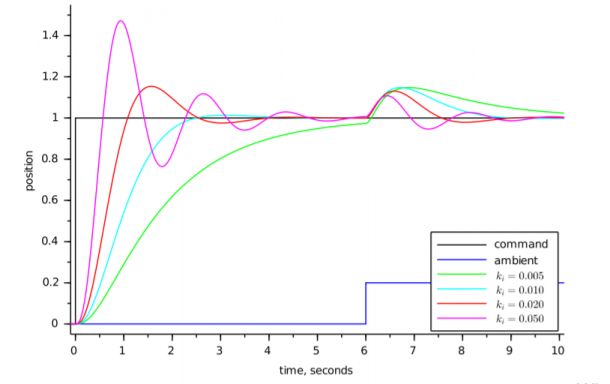
İntegral error değerinin alanını bulmak anlamına gelir. Bu işlem her bir periyottaki error katsayı (Ki)değeri ile çarpılarak toplanır. Setpoint değerinin altında yaptığı error değerinin alanı kadar setpoint değerinin üst kısmında da salınım yapar. İntegral çok fazla artmadan sınırlandırılması gerekir. Sürekli toplandığı için integral çok artarsa tekrar azalmasını beklemek zaman alır. Bu yüzden integrali sınırlamak sistemin çabuk toparlamasını sağlayacaktır.
- Sadece integral ile kontrol yapılırsa toplam error değeri kadar setpoint değerinin üstüne çıkar. Setpoint üzerinde toplam error değerini tekrar hesaplar ve setpoint altında toplam error değeri kadar salınım yapar. Bu nedenle sonsuz bir osilasyon değeri elde edilir.
- Eğer (Kp) değeri ile (Ki) değeri aynı anda hesaplanırsa başlangıçtan setpoint değerine kadar (Ki) değeri, sürekli error değerlerini toplama içerisinde olduğu için büyük bir error değeri oluşacaktır. Bu nedenle (Kp) değerini belirli bir noktaya getirip, (Ki) değerini (Kp) değerinden sonra başlatmanız gerekir. Böylece oluşacak salınımlar büyük oranda azaltılmış olur.
Derivative Kontrol
D=Kd*Error (d/dt)
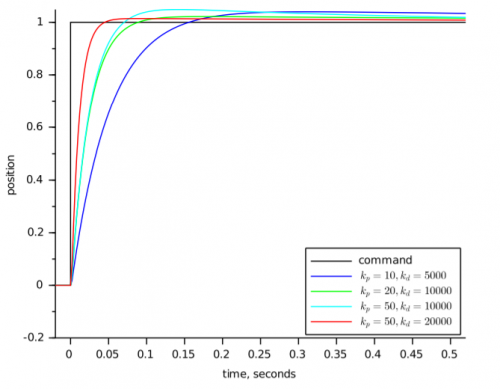
Derivative zamana bağlı değerin değişimi ile ilgilidir. Sistemde gerçekleşen değişim sırasında gerçekleşecek değişimi fark eder ve sistemi istenen değerin üzerine çıkmaması için yavaşlatır.
PID Kontrol Grafiği
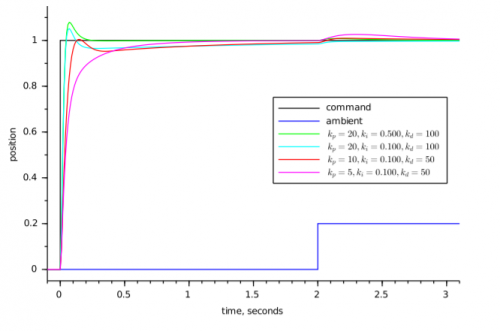
Şekil 6'da Proportional, Integral ve Derivative kulanılmıştır. Verilen grafikte değişken bir ortamda (Kp), (Ki) ve (Kd) katsayılarına farklı değerler verilerek sinyallerin oluşturduğu hareketler gözlenmiştir.